Esercizi per la classe 5°

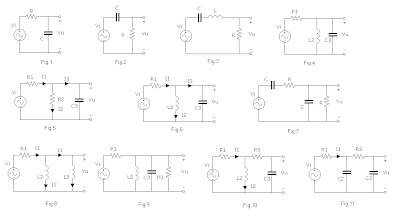
Nella figura precedente sono indicati vari circuiti in cui bisogna trovare la f.d.t Vo/Vi

1-2-3) Procedimento: uso il partitore di tensione ponendo al numeratore l'impedenza su cui raccolgo la tensione di uscita e al denominatore la somma delle impedenze del circuito

4-5-6-7-8-9) Procedimento: uso Millmann oppure dopo avere calcolato il parallelo dell'impedenza sull'uscita faccio il partitore

10-11) Procedimento: Uso Millmann per calcolare la tensione tra il nodo centrale e la massa poi uso il partitore per determinare la tensione di uscita

RNTS1:

N.B. Applicare la sequenza di operazioni indicata nella figura

Sapendo Ri=20K, Re=0.56K, Rf=33K, Avo=800;Ro=4.7K e RL=5.6K determinare Avf, Rif e Rof

e verificare che Avf è prossimo al valore 1/beta

Sapendo Ri=20K, Re=1.2K, Rf=33K, Avo=800;fl=450Hz, fh=300KHz, Ro=4.7K e RL=5.6K determinare Avf, flf, fhf, Rif e Rof e verificare che Avf è prossimo al valore 1/beta

Sapendo Ri=20K, Re=1.2K, Rf=33K, Avo=800;fl=450Hz, fh=300KHz, Ro=4.7K e RL=5.6K determinare Avf, flf, fhf, Rif e Rof e verificare che Avf è prossimo al valore 1/beta

Osc1:

Disegnare un oscillatore a ponte di Wien che oscilla a 5Khz. I condensatori hanno valore di 22nF e la R che collega il terminale invertente a massa vale 2.2K. Determinare i valori delle altre R.


Disegnare un oscillatore a ponte di Wien, sapendo che C=10nF e R=4.7K mentre la R che collega l'uscita al terminale invertente vale 6.8K. Trovare la frequenza di oscillazione e l'altra R.

Procedimento: Basta aprire l'anello sul + dell'operazionale, calcolare beta ed A in forma letterale usando la frequenza complessa s, annullare la parte reale del denominatore del beta in modo che il beta diventi reale e con il suo reciproco si calcola il valore di A e quindi i valori delle resistenze.

Osc2:

In un oscillatore aprendo l'anello si calcola che il beta è dato dalla espressione 2RCS/[(RCS)^2 + 3 RCS +6] con C=10nF e R=2.2K. Trovare la frequenza di oscillazione e il valore minimo di A necessario per il suo funzionamento

Procedimento: per w basta annullare la parte reale del denominatore di beta e una volta fatto va invertito per trovare A

Osc4: Dato un oscillatore di Colpitts in cui l'amplificazione vale -8 e i C di uscita 2nF sapendo che oscilla 100Khz determinare il valore di L e del condensatore in ingresso.

Osc5: Dato un oscillatore di Hartley in cui L1=1uH e L2=2.2uH trovare la frequenza di oscillazione e il valore della amplificazione sapendo che C=100pF

Procedimento: qui si parte sempre dal teorema dei tre punti, scrivendo le espressioni delle impedenze si calcola w e scrivendo beta si calcola poi A.

Osc6: Dato un oscillatore a sfasamento in cui C=10nF e R=2.2K trovare l'amplificazione minima e la frequenza di oscillazione.

Procedimento: beta= (RCS)^3/[(RCS)^3+6(RCS)^2+5RCS+1] per cui si annulla la parte reale del denominatore per trovare w e invertendo il valore d beta si trova A

Osc7: Progettare un astabile con Ne555 in cui la f=4KHz e il d.c. sia del 60%

Procedimento: Sulla base dello schema scelto si trovano le costanti di tempo di carica e scarica, con queste si trovano i tempi in cui l'impulso resta alto e basso.

Osc7: Ripetere con d.c. del 25%

Osc8: Progettare un astabile con OA in modo che la f=5KHz e il d.c. sia del 50% con Vcc=18V.

Procedimento: Sulla base dello schema scelto si trovano le costanti di tempo di carica e scarica, con queste si trovano i tempi in cui l'impulso resta alto e basso.

Osc9: Ripetere con d.c. del 25% e del 70%

Osc10: Progettare un monostabile con OA , completo del circuito di comando, che produca un uscita un impulso di 3ms, con Vcc=18V. Dire anche il valore minimo della frequenza dell'onda quadra utilizzabile per la commutazione.

Osc11: Progettare un monostabile con Ne555, completo del circuito di comando, che produca un uscita un impulso di 3ms. Dire anche il valore minimo della frequenza dell'onda quadra utilizzabile per la commutazione.

Osc12: Progettare un generatore di onda triangolare che produca una tensione max di 10V alla frequenza di 3KHz con Vcc=18V.


Per i filtri vanno ricordate le formule da cui ottenere i parametri di progetto:

Passa basso:

A(s)= Ao/[(s^2/w^2)+2z(s/w)+1] (f.d.t. generale)

A(s)= K/[(RCs)^2+(3-k)RCs+1] con K=1+Ra/Rb (f.d.t. specifica del filtro VCVS)

Passa Alto:

A(s)= Ao (s/w)^2/[(s^2/w^2)+2z(s/w)+1]

A(s)= K(RCs)^2/[(RCs)^2+(3-k)RCs+1] con K=1+Ra/Rb


Passa Banda:

A(s)= 2zAo(s/w)/[(s^2/w^2)+2z(s/w)+1]

A(s)= K(RCs)/[(RCs)^2+(4-k)RCs+2] con K=1+Ra/Rb


N.B. I valori di z e F necessari per i progetti si trovano nelle tabelle sul libro

Il modo per procedere nello svolgimento degli esercizi in cui si progetta un filtro è questo:

1) disegno dello schema elettrico contrasseganto dai nomi dei componenti da determinare
2) determinare le relazioni tra parametri del filtro (w,z,Ao) e i valori dei componenti circuitale (le varie R e C del circuito) dal confronto tra la f.d.t generale e quella specifica del circuito
3) se necessario trovare nella tabella i valori di progetto del filtro (F e z) e quindi le fo naturali
4) calcolare le R e la C del circuito da progettare


Filtr1: Progettare un filtro del I° ordine passa basso con amplificazione di 3 e ft=2KHz

Filtr2: Progettare un filtro del I° ordine passa alto con amplificazione di 2.5 e ft=5KHz

Filtr3: Progettare un filtro del I° ordine passa alto con amplificazione di 4dB e ft=1KHz


Filtr4: Progettare un filtro del II° ordine passa basso alla Butterwotrh e ft=5KHz

Filtr5: Progettare un filtro del II° ordine passa basso alla Butterwotrh con amplificazione di 5dB e ft=3KHz

Filtr6: Progettare un filtro del II° ordine passa alto alla Butterwotrh con amplificazione di 2.5 e ft=4KHz

Filtr7: Progettare un filtro del II° ordine passa basso alla Chebyshev con ft=4KHz

Filtr8: Progettare un filtro del II° ordine passa alto alla Chebyshev con ft=3KHz

Filtr9: Progettare un filtro del II° ordine passa alto alla Chebyshev con ft=3KHz e guadagno 6dB

Filtr10: Progettare un filtro del II° ordine passa basso alla Bessel con ft=3KHz

Filtr11: Progettare un filtro del II° ordine passa basso alla Bessel con ft=3KHz con guadagno 8dB

Filtr12: Progettare un filtro del III° ordine passa basso alla Butterworth con ft=3KHz e guadagno 4dB

Filtr13: Progettare un filtro del III° ordine passa alto alla Butterworth con ft=4KHz e guadagno 4dB

Filtr14: Progettare un filtro del III° ordine passa basso alla Chebyshev con ft=4KHz e guadagno 4dB

Filtr15: Progettare un filtro del III° ordine passa alto alla Bessel con ft=4KHz e guadagno 4dB



Filtr20: Progettare un filtro passa banda (banda stretta) fo=4KHz e guadagno 4dB

Filtr21: Progettare un filtro passa banda (banda stretta) fo=4KHz e Q=5

Filtr22: Progettare un filtro passa banda (banda stretta) fo=5KHz e banda di 2 Khz

Filtr23: Progettare un filtro passa banda a due stadi (banda stretta) con fo=4KHz e Q=5



Filtr30: Progettare un filtro passa banda in banda larga (del II° ordine) con fl=1KHz e fh=12Khz

Filtr31: Progettare un filtro passa banda in banda larga (del II° ordine) a due stadi con fl=1KHz e banda 12Khz


Filtr40: Progettare un filtro escludi banda (in banda stretta) con fo=3Khz e Q=3

Filtr41: Progettare un filtro escludi banda (in banda stretta) con fo=5Khz e B=2kHz

Filtr42: Progettare un filtro escludi banda (in banda larga) con fl=1Khz e B=10kHz

Filtr43: Progettare un filtro escludi banda (in banda larga) con fl=1Khz e fh=11Khz

Ricordare per la potenza le seguenti definizioni distingendo la grandezze statiche da quelle dinamiche: Pcc, Pd, PL, Vceq, Icq, Pu, F, eta, THD o Dtot, Icm, Vcem, VLm e ILm

Gli esercizi vanno svolti usando il grafico stilizzato delle caratterstiche di uscita per individuare la posizione del punto di riposo.

Una volta determinato il punto di riposo diseganrela retta di carico statica e dinamica e quindi determinare il valore vcem che il punto di riposo in esame permette senza distorsioni o tagli

Pot1: Trovare il punto di riposo di un BJT che alimenta un carico Rc percorso da corrente con Vcc=12V, Rc=8 Ohm, Beta=40, RB=0.5K e il valore massimo per l'oscillazione considerando Vcesat=0V. Calcolare anche Pd, PL, F ed eta.

Pot2: Trovare il punto di riposo di un BJT che alimenta un carico Rc percorso da corrente con Vcc=15V, Rc=8 Ohm, Beta=50, RB=0.82K e il valore massimo per l'oscillazione considerando Vcesat=1.5V. Calcolare anche Pd, PL, F ed eta.

Pot3: Trovare il punto di riposo di un BJT che alimenta un carico Rc percorso da corrente con Vcc=15V, Rc=8 Ohm, Re=1Ohm, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=1V . Calcolare anche Pd, PL, F ed eta.

Pot4: Trovare il punto di riposo di un BJT che alimenta un carico Rc percorso da corrente con Vcc=15V, Rc=4 Ohm, Re=2Ohm, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=1V. Calcolare anche Pd, PL, F ed eta.

Pot5: Trovare il punto di riposo di un BJT che alimenta un carico RL non percorso da corrente con Vcc=15V, RL=4 Ohm, Re=0Ohm, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=0V. Calcolare anche Pd, PL, F ed eta.

Pot6: Trovare il punto di riposo di un BJT che alimenta un carico RL non percorso da corrente con Vcc=15V, RL=4 Ohm, Re=2Ohm, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=1V. Calcolare anche Pd, PL, F ed eta.

Pot10: Trovare il punto di riposo di un BJT che alimenta un carico RL con accoppiamento a trasformatore con Vcc=15V, RL=4 Ohm, n=2, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=1V. Calcolare anche Pd, PL, F ed eta.

Pot11: Trovare il punto di riposo di un BJT che alimenta un carico RL con accoppiamento a trasformatore con Vcc=15V, RL=8 Ohm, n=3.2, Re=2Ohm, Beta=80, RB=0.56K e il valore massimo per l'oscillazione considerando Vcesat=1V. Calcolare anche Pd, PL, F ed eta.